V

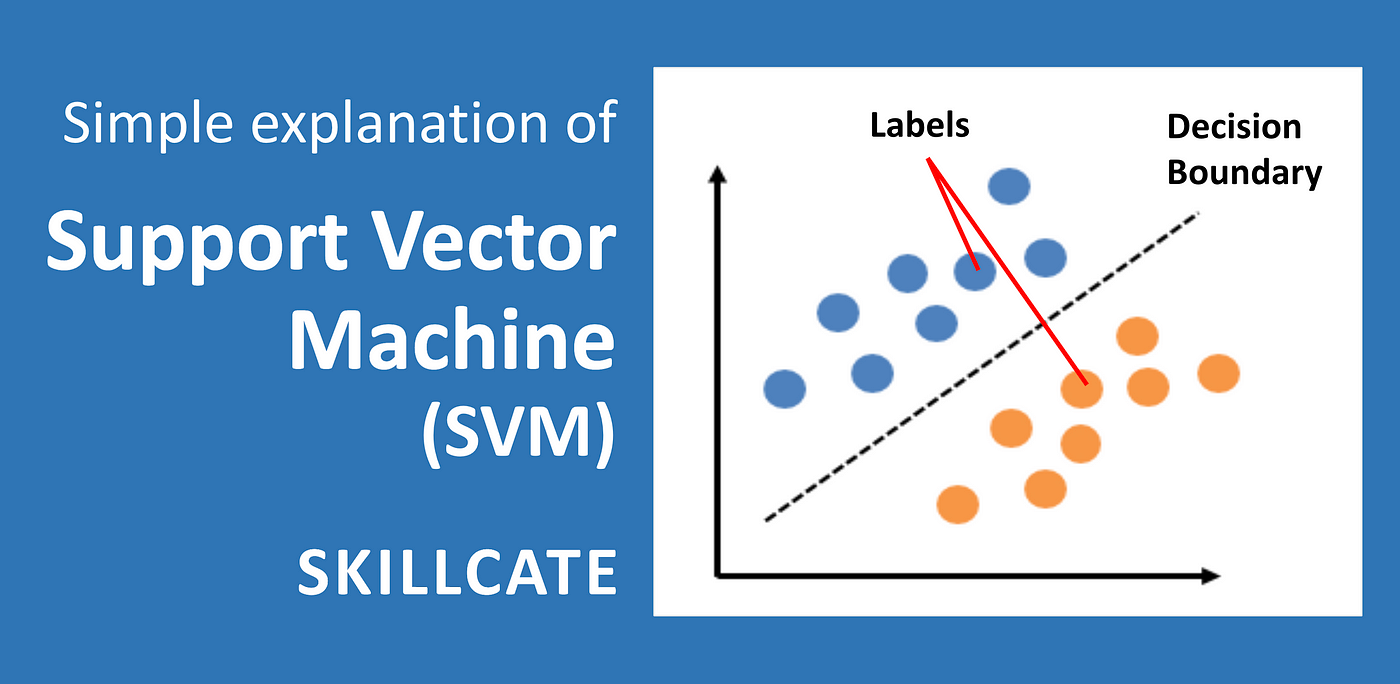
ladimir N Vapnik, seorang Professor dari Columbia, Amerika Serikat pada tahun 1992 memperkenalkan sebuah algoritma training yang bertujuan untuk memaksimalkan margin antara pola pelatihan dan batas keputusan (decision boundary) [10]. Algoritma ini kemudian dikenal luas sebagai Support Vector Machine (SVM).

Support Vector Machine adalah model ML multifungsi yang dapat digunakan untuk menyelesaikan permasalahan klasifikasi, regresi, dan pendeteksian outlier. Termasuk ke dalam kategori supervised learning, SVM adalah salah satu metode yang paling populer dalam machine learning. Siapa pun yang tertarik untuk masuk ke dalam dunia ML, perlu mengetahui SVM.

Tujuan dari algoritma SVM adalah untuk menemukan hyperplane terbaik dalam ruang berdimensi-N (ruang dengan N-jumlah fitur) yang berfungsi sebagai pemisah yang jelas bagi titik-titik data input.

Gambar di sebelah kiri menunjukkan beberapa kemungkinan bidang (hyperplane) untuk memisahkan data lingkaran dan data kotak. Algoritma SVM kemudian mencari hyperplane terbaik yang dapat memisahkan kedua kelas secara optimal. Seperti tampak pada gambar di sebelah kanan, sebuah hyperplane optimal berhasil dibuat dan mampu memisahkan kedua kelas sehingga memiliki margin yang maksimal.

Beberapa keunggulan Support Vector Machine antara lain:

1. SVM efektif pada data berdimensi tinggi (data dengan jumlah fitur atau atribut yang sangat banyak).
2. SVM efektif pada kasus di mana jumlah fitur pada data lebih besar dari jumlah sampel.
3. SVM menggunakan subset poin pelatihan dalam fungsi keputusan (disebut support vector) sehingga membuat penggunaan memori menjadi lebih efisien.

Support Vector Machine Classifier

Untuk memahami bagaimana algoritma support vector machine atau SVM bekerja pada kasus klasifikasi, bayangkan kita memiliki sebuah kebun binatang mini. Di kebun binatang tersebut terdapat dua jenis binatang yaitu, ayam hias dan ular. Sebagai seorang ML engineer, kita ingin mengembangkan sebuah model yang mampu membedakan antara ayam dan ular piton agar bisa menempatkan kedua hewan tersebut di kandang yang berbeda. Kita tentunya tak mau menyatukan ayam dan ular dalam satu kandang yang sama ya.

Kita bisa membuat sebuah model klasifikasi yang memisahkan antara kedua kelas tersebut menggunakan Support Vector Machine. Menurut Aurelien Geron dalam buku Hands on Machine Learning, SVM bekerja dengan membuat decision boundary atau sebuah bidang yang mampu memisahkan dua buah kelas. Pada masalah ini decision boundary yang mampu memisahkan kelas ayam dan kelas ular adalah sebuah garis lurus yang dapat dilihat pada gambar.

Lantas bagaimana SVM membuat sebuah decision boundary tersebut?

Pertama SVM mencari support vector pada setiap kelas. Support vector adalah sampel dari masing-masing kelas yang memiliki jarak paling dekat dengan sampel kelas lainnya. Pada contoh dataset bola basket dan bola kaki di bawah, support vector adalah bola basket dan bola kaki yang memiliki warna biru.

Setelah support vector ditemukan, SVM menghitung margin. Margin bisa kita anggap sebagai jalan yang memisahkan dua kelas. Margin dibuat berdasarkan support vector di mana support vector bekerja sebagai batas tepi jalan, atau sering kita kenal sebagai bahu jalan. SVM mencari margin terbesar atau jalan terlebar yang mampu memisahkan kedua kelas.

Pada dataset bola basket dan bola kaki di atas SVM akan memilih margin di sebelah kanan karena ‘jalan’ atau margin pada gambar sebelah kanan lebih lebar dari ‘jalan’ di sebelah kiri. Oleh karena itu, gambar sebelah kanan disebut sebagai high margin classification dan gambar di sebelah kiri disebut low margin classification.

Kembali lagi ke kasus klasifikasi ayam dan ular, sampel ayam dan ular yang berada dalam lingkaran merah adalah support vector. Kemudian kita mencari jalan terlebar dari 2 support vector. Setelah menemukan jalan terlebar, decision boundary lalu digambar berdasarkan jalan tersebut.

Decision boundary adalah garis yang membagi jalan atau margin menjadi 2 bagian yang sama besar. Hyperplane adalah bidang yang memisahkan kedua kelas, sedangkan margin adalah lebar ‘jalan’ yang membagi kedua kelas. Selamat! Sekarang Anda sudah paham bagaimana support vector machine bekerja dalam masalah klasifikasi.

SVM Klasifikasi non Linier

Sebelumnya kita sudah belajar tentang support vector classifier untuk kasus linear. Support vector classifier bekerja dengan mencari margin terbesar, atau jalan terlebar yang mampu untuk memisahkan 2 buah kelas. Permasalahannya, data di lapangan jauh lebih kompleks dibanding data ayam hias dan ular seperti di atas. Bagaimana jika data yang kita miliki terlihat seperti ini?

Data di atas merupakan data yang tidak bisa dipisahkan secara linier sehingga kita menyebutnya sebagai data non-linear. Pada data non-linear, decision boundary yang dihitung algoritma SVM bukan berbentuk garis lurus. Meski cukup rumit dalam menentukan decision boundary pada kasus ini, tapi kita juga mendapatkan keuntungan, yaitu, bisa menangkap lebih banyak relasi kompleks dari setiap data poin yang tersebar.

Untuk data seperti di atas, Support Vector Classifier menggunakan sebuah metode yaitu “kernel trick” sehingga data dapat dipisahkan secara linier. Apa itu trik kernel? Ia adalah sebuah metode untuk mengubah data pada dimensi tertentu (misal 2D) ke dalam dimensi yang lebih tinggi (3D) sehingga dapat menghasilkan hyperplane yang optimal. Perhatikan gambar berikut.

Bagaimana trik kernel bekerja?

Pertama, kita perlu menghitung skor jarak dari dua titik data, misal x_i dan x_j. Skor akan bernilai lebih tinggi untuk titik data yang lebih dekat, dan sebaliknya. Lalu kita gunakan skor ini untuk memetakan data pada dimensi yang lebih tinggi (3D). Teknik ini berguna untuk mengurangi waktu dan sumber daya komputasi, terutama untuk data berjumlah besar. Hal ini juga mencegah kebutuhan akan proses transformasi yang lebih kompleks. Itulah mengapa teknik ini sering disebut sebagai trik kernel.

Seperti yang ditunjukkan gambar di atas, pemetaan titik data dari ruang 2D menjadi 3D menggunakan fungsi kernel. Titik-titik merah yang sebelumnya berada di tengah sekarang berada di dalam bidang vertikal dengan posisi lebih rendah setelah diubah menjadi ruang 3D. Titik data yang sebelumnya sulit dipisahkan, sekarang dapat dengan mudah dipisahkan dengan teknik kernel.

Mari perhatikan ilustrasi berikut tentang bagaimana trik kernel bekerja pada data yang lebih sederhana.

Data di atas adalah data 1 dimensi dengan 2 buah kelas yaitu dokter dan polisi. Data di atas bukan data linier karena kita tak dapat menggambar satu garis lurus untuk memisahkan 2 kelas yang ada. Bagaimana cara kita bisa menggambar garis lurus yang bisa memisahkan 2 kelas tersebut? Betul, kita akan menggunakan trik kernel untuk mengubah data tersebut ke dalam dimensi yang lebih tinggi seperti ke dalam bidang 2 dimensi.

Ketika data sudah diubah ke dalam bidang 2 dimensi, sebuah garis lurus bisa digambar untuk memisahkan 2 kelas. Trik kernel menggunakan fungsi matematis yang bisa mengubah data dari dimensi tertentu ke dimensi yang lebih tinggi sehingga kelas-kelas pada data dapat dipisah secara linier.

Berikut adalah beberapa fungsi kernel yang perlu Anda ketahui.

• Linear
• RBF (Radial Basis Function) atau Gaussian kernel
• Polinomial
• Sigmoid

Bagaimana SVM Classifier ini diterapkan dalam kehidupan sehari-hari?

Salah satu contoh aplikasi SVM dalam kehidupan sehari-hari adalah fitur deteksi wajah. Pengenalan wajah telah berkembang menjadi topik penelitian utama dalam bidang computer vision. Sistem pengenalan wajah memiliki banyak fitur/kelas (individu) dan hanya memiliki beberapa data gambar (sampel) per orang, bahkan kadang hanya ada satu sampel pelatihan untuk setiap orang. Permasalahan dengan jumlah fitur lebih banyak dari jumlah sampel ini efektif jika dipecahkan dengan algoritma SVM.

Aplikasi lain SVM yang juga menarik adalah di bidang bioinformatika. Dalam bidang komputasi biologi, deteksi homologi jarak jauh pada protein (protein remote homology detection) adalah permasalahan yang umum. Metode paling efektif untuk menyelesaikan permasalahan ini adalah dengan SVM. Dalam beberapa tahun terakhir, algoritma SVM telah diterapkan secara luas untuk proses deteksi ini. Fungsi kernel pada SVM digunakan untuk mengidentifikasi sekuens biologis dan membantu menemukan kesamaan antara urutan protein yang berbeda.

SVM untuk Klasifikasi Multi-kelas

SVM sejatinya merupakan binary classifier atau model untuk klasifikasi 2 kelas. Namun, SVM juga dapat dipakai untuk klasifikasi multi-kelas menggunakan suatu teknik yaitu “one-vs-rest”.

Pada masalah klasifikasi multi-kelas, SVM melakukan klasifikasi biner untuk masing-masing kelas. Model kemudian memisahkan kelas tersebut dari semua kelas lainnya, menghasilkan model biner sebanyak jumlah kelasnya. Untuk membuat prediksi, semua proses klasifikasi biner dijalankan pada tahap uji.

Sebagai contoh, jika ada 3 buah kelas: donat, ayam, dan burger, SVM akan melakukan 3 kali klasifikasi. Pertama, membangun pemisah antara kelas donat dan kelas bukan donat.

Kemudian membangun pemisah antara kelas ayam dan kelas bukan ayam, lalu pemisah antara kelas burger dan bukan kelas burger. Teknik inilah yang disebut dengan “One-vs-Rest”.

Support Vector Regression

Seperti yang telah disebutkan di awal modul, selain bisa menyelesaikan masalah klasifikasi, support vector juga bisa dipakai untuk prediksi data kontinu yaitu kasus regresi.

Support Vector Regression (SVR) menggunakan prinsip yang sama dengan SVM pada kasus klasifikasi. Perbedaannya adalah jika pada kasus klasifikasi, SVM berusaha mencari ‘jalan’ terbesar yang bisa memisahkan sampel-sampel dari kelas berbeda, maka pada kasus regresi SVR berusaha mencari jalan yang dapat menampung sebanyak mungkin sampel di ‘jalan’.

Perhatikan gambar berikut untuk melihat contoh SVR [4].

Seperti dijelaskan oleh Garon dalam Hands-On Machine Learning with Scikit Learn [4], gambar di atas menunjukkan dua model Regresi SVM linier yang dilatih pada beberapa data linier acak, satu dengan margin besar (ϵ = 1,5) dan yang lainnya dengan margin kecil (ϵ = 0,5). Lebar jalan dikontrol oleh hyperparameter ϵ, yang juga disebut maksimum eror. Menambahkan data training ke dalam margin tidak akan mempengaruhi prediksi model. Oleh karena itu, model disebut sebagai ϵ-insensitivity (tidak sensitif-ϵ).

Berbeda dengan SVM di mana support vector adalah 2 sampel dari 2 kelas berbeda yang memiliki jarak paling dekat, pada SVR support vector adalah sampel yang menjadi pembatas jalan yang dapat menampung seluruh sampel pada data. M. Awad dan R. Khanna dalam bab 4 bukunya [14] mengilustrasikan support vector pada SVR sebagai berikut.

Mari kita ambil contoh implementasi SVR pada kasus prediksi harga rumah di kota Boston, Amerika Serikat, menggunakan dataset yang sangat populer untuk kasus regresi: “Boston Housing Price.csv”. Pertama, kita akan melihat bagaimana hasil prediksi regresi linear sederhana pada data ini, kemudian kita akan membandingkan hasilnya dengan SVR.

Sedikit mengingat kembali tentang regresi linear yang telah diulas di modul sebelumnya, ukuran performa untuk permasalahan regresi linear adalah Root Mean Square Error (RMSE). RMSE memberi gambaran tentang seberapa banyak kesalahan dalam prediksi yang dibuat oleh sistem. Tujuannya tentu saja untuk mendapatkan eror atau tingkat kesalahan seminimal mungkin.

Pada kasus prediksi harga rumah di Boston, regresi linear akan memberikan hasil plot sebagai berikut.

Mari kita coba implementasikan SVR pada dataset yang sama. Salah satu kelebihan SVR dibanding regresi linear adalah SVR memberi kita fleksibilitas untuk menentukan seberapa banyak kesalahan yang dapat diterima dalam model kita. Algoritma SVR akan menemukan garis yang cocok (hyperplane) agar sesuai dengan data. Kita bisa mengatur parameter ϵ untuk mendapatkan akurasi model yang kita inginkan.

Jika kita pilih nilai ϵ = 5 dan kita plot datanya, hasilnya adalah sebagai berikut.

Garis merah pada gambar menunjukkan garis regresi, sedangkan garis biru menunjukkan margin dari eror, ϵ, yang telah kita atur nilainya tadi dengan ϵ = 5 (atau dalam skala ribuan berarti senilai $ 5,000).

Dari gambar di atas Anda mungkin bisa langsung melihat bahwa algoritma SVR ini tidak bisa memberikan hasil prediksi yang baik untuk seluruh data sebab beberapa titik masih berada di luar batas. Oleh karena itu, kita perlu menambahkan parameter lain pada algoritma yaitu parameter C yang disebut sebagai regularization parameter atau parameter keteraturan. Ada juga yang menyebutnya slack parameter. Jui Yang Hsia dan Chih-Jen Lin dalam tulisannya [15] menyatakan bahwa regularization parameter ini berfungsi untuk menghindari overfitting pada training data.

Kembali pada kasus prediksi rumah di Boston, mari kita coba tambahkan parameter C pada data. Jika kita set nilai C = 2.0, lantas hasilnya adalah sebagai berikut.

Perhatikan bahwa sekarang model kita menyesuaikan sebaran data dengan lebih baik dibanding model sebelumnya.

Ada dua parameter yang kita gunakan dalam model SVR, yaitu parameter ϵ yang menunjukkan margin of error dan parameter C yang merupakan parameter keteraturan atau regularization parameter.

Ada tiga jenis implementasi Support Vector Regression pada scikit-learn yaitu: SVR, NuSVR, dan LinearSVR. Implementasi dari LinearSVR lebih cepat dari SVR tetapi hanya dapat digunakan untuk kernel linear, sedangkan NuSVR mengimplementasikan formula yang sedikit berbeda dari SVR dan LinearSVR. NuSVR menggunakan parameter nu untuk mengontrol jumlah support vector. Jika tertarik untuk lebih memahami bagaimana implementasi SVR pada scikit-learn, Anda bisa mengunjungi tautan berikut: SVR, NuSVR, dan LinearSVR.